Back
Present
Facts for Kids
The area of a triangle can be calculated using various formulas depending on the information available, including base and height, side lengths, or vertex coordinates.
Explore the internet with AstroSafe
Search safely, manage screen time, and remove ads and inappropriate content with the AstroSafe Browser.
Download
Inside this Article
Equilateral Triangle
Pythagorean Theorem
Rectangle
Triangle
Mountain
Geometry
Formula
School
Square
Did you know?
🔺 The area ( A ) of a triangle can be calculated using the formula ( A = rac{1}{2} imes ext{base} imes ext{height} ).
📏 In a right triangle, the area can also be expressed as ( A = rac{1}{2} imes a imes b ), where ( a ) and ( b ) are the legs of the triangle.
📐 For an equilateral triangle, the area can be computed using ( A = rac{sqrt{3}}{4} imes s^2 ), where ( s ) is the length of a side.
🧮 The formula for the area can also be represented using Heron's formula as ( A = sqrt{s(s-a)(s-b)(s-c)} ), where ( s ) is the semi-perimeter.
✨ The semi-perimeter ( s ) is calculated as ( s = rac{a+b+c}{2} ) in Heron's formula.
📉 The altitude of a triangle must be drawn perpendicularly from a vertex to the opposite side to correctly use the area formula.
📊 The area of a triangle is independent of the triangle's orientation; it only depends on the base and height measurements.
💡 For two triangles with equal bases and heights, their areas will also be equal, regardless of their shapes.
🏗️ The area can also be determined if all three sides are known using the formula derived from Heron’s formula.
🌐 A triangle's area can also be derived using coordinates of its vertices with the formula ( A = rac{1}{2} |x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2)| ).
Show Less
Become a Creator with DIY.org
A safe online space featuring over 5,000 challenges to create, explore and learn in.
Learn more
Overview
Welcome to the world of triangles! 🛶
Triangles are three-sided shapes that are everywhere around us. They can be seen in buildings, bridges, and even in your pizza slice! 🍕
Each triangle has three corners called vertices and three sides. You might find triangles in different types, like equilateral, isosceles, and scalene. Understanding how to calculate the area of a triangle helps us know how much space is inside! 🌌
Today, we will learn all about triangles, especially how to find their areas with fun facts and activities!
Triangles are three-sided shapes that are everywhere around us. They can be seen in buildings, bridges, and even in your pizza slice! 🍕
Each triangle has three corners called vertices and three sides. You might find triangles in different types, like equilateral, isosceles, and scalene. Understanding how to calculate the area of a triangle helps us know how much space is inside! 🌌
Today, we will learn all about triangles, especially how to find their areas with fun facts and activities!
Read Less
Historical Background
Did you know that triangles have been studied for thousands of years? 📜
Ancient Egyptians built the Pyramids using triangles. The famous mathematician Pythagoras (circa 570-495 BC) discovered many triangle properties and the Pythagorean theorem, which explains relationships between triangle sides. 📐
Archimedes, a great mathematician from ancient Greece, also studied triangle areas. In Asia, the Indian mathematician Brahmagupta (598-668 AD) worked with triangle areas too! Today, we still use ideas from these brilliant minds in math and engineering. How cool is that? 🌍
Ancient Egyptians built the Pyramids using triangles. The famous mathematician Pythagoras (circa 570-495 BC) discovered many triangle properties and the Pythagorean theorem, which explains relationships between triangle sides. 📐
Archimedes, a great mathematician from ancient Greece, also studied triangle areas. In Asia, the Indian mathematician Brahmagupta (598-668 AD) worked with triangle areas too! Today, we still use ideas from these brilliant minds in math and engineering. How cool is that? 🌍
Read Less
Definition of a Triangle
A triangle is a flat shape with three straight sides and three angles. 🦋
The three sides can be different lengths! The three corners, or vertices, are named with letters, like A, B, and C. The longest side is called the base, usually at the bottom. For example, a triangle with all sides equal is an equilateral triangle, while one with two sides the same is an isosceles triangle. Did you know the smallest triangle has a side length as little as 1 cm? 🌟
Triangles are important in math because they help us understand shapes better!
The three sides can be different lengths! The three corners, or vertices, are named with letters, like A, B, and C. The longest side is called the base, usually at the bottom. For example, a triangle with all sides equal is an equilateral triangle, while one with two sides the same is an isosceles triangle. Did you know the smallest triangle has a side length as little as 1 cm? 🌟
Triangles are important in math because they help us understand shapes better!
Read Less
Related Geometric Concepts
Triangles are part of a family called polygons. 🌈
Polygons are flat shapes with straight sides. The most famous polygon is a square, which is a type of rectangle. 🟦
Another great concept is angles—there are three angles in every triangle! A triangle can have acute angles (less than 90°), right angles (exactly 90°), or obtuse angles (more than 90°). 🧭
Learning about triangles introduces you to other shapes like quadrilaterals (four sides) and circles. All these shapes work together in math to create fun geometry puzzles! 🎊
Polygons are flat shapes with straight sides. The most famous polygon is a square, which is a type of rectangle. 🟦
Another great concept is angles—there are three angles in every triangle! A triangle can have acute angles (less than 90°), right angles (exactly 90°), or obtuse angles (more than 90°). 🧭
Learning about triangles introduces you to other shapes like quadrilaterals (four sides) and circles. All these shapes work together in math to create fun geometry puzzles! 🎊
Read Less
Formula for Area Calculation
To calculate the area of a triangle, we use a special formula:
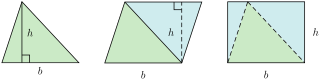
Area = (Base × Height) ÷ 2. 📏
In this formula, the base is the bottom side of the triangle, and the height is how tall the triangle stands from the base to the top point. Imagine a triangle where the base is 4 cm and the height is 3 cm. To find the area, you would multiply 4 cm × 3 cm to get 12 and then divide it by 2. So, the area would be 6 square centimeters! 🧮
Wow!
Area = (Base × Height) ÷ 2. 📏
In this formula, the base is the bottom side of the triangle, and the height is how tall the triangle stands from the base to the top point. Imagine a triangle where the base is 4 cm and the height is 3 cm. To find the area, you would multiply 4 cm × 3 cm to get 12 and then divide it by 2. So, the area would be 6 square centimeters! 🧮
Wow!
Read Less
Examples of Area Calculations
Let’s practice some area calculations! 😃
Imagine a triangle with a base of 5 cm and a height of 4 cm. Using our formula, we find:
Area = (5 cm × 4 cm) ÷ 2 = 20 ÷ 2 = 10 square centimeters!
Now try a triangle with a base of 10 cm and a height of 3 cm:
Area = (10 cm × 3 cm) ÷ 2 = 30 ÷ 2 = 15 square centimeters!
What about a triangle with a base of 8 cm and a height of 6 cm?
Area = (8 cm × 6 cm) ÷ 2 = 48 ÷ 2 = 24 square centimeters! Good job! 🥳
Imagine a triangle with a base of 5 cm and a height of 4 cm. Using our formula, we find:
Area = (5 cm × 4 cm) ÷ 2 = 20 ÷ 2 = 10 square centimeters!
Now try a triangle with a base of 10 cm and a height of 3 cm:
Area = (10 cm × 3 cm) ÷ 2 = 30 ÷ 2 = 15 square centimeters!
What about a triangle with a base of 8 cm and a height of 6 cm?
Area = (8 cm × 6 cm) ÷ 2 = 48 ÷ 2 = 24 square centimeters! Good job! 🥳
Read Less
Interactive Learning Activities
Let’s make learning triangles fun! 🎨
1. Triangle Hunt: Go on a treasure hunt to find triangles around your house or school! Look for objects like sandwiches, road signs, or toys! 📦
2. Paper Triangles: Cut out triangles out of colored paper. Measure their bases and heights, then calculate their areas together! 📐
3. Draw Your Own: Get creative and draw your own triangles with different side lengths. Calculate their areas! 🖍
️
4. Online Games: Look for fun games that let you solve triangle problems or explore shapes interactively. Learning can be a blast! 🎮
Enjoy the adventure with triangles! 🌟
1. Triangle Hunt: Go on a treasure hunt to find triangles around your house or school! Look for objects like sandwiches, road signs, or toys! 📦
2. Paper Triangles: Cut out triangles out of colored paper. Measure their bases and heights, then calculate their areas together! 📐
3. Draw Your Own: Get creative and draw your own triangles with different side lengths. Calculate their areas! 🖍
️
4. Online Games: Look for fun games that let you solve triangle problems or explore shapes interactively. Learning can be a blast! 🎮
Enjoy the adventure with triangles! 🌟
Read Less
Different Methods to Calculate Area
There are several ways to calculate the area of a triangle! 😄
You can use the basic formula mentioned earlier, but you can also explore other methods! For example:
1. Heron’s Formula: This is useful if you know all three side lengths! First, find the semi-perimeter (s = (a + b + c) ÷ 2) and then use the formula Area = √(s × (s - a) × (s - b) × (s - c)).
2. Coordinate Geometry: If you know the vertices' coordinates, you can use the formula involving coordinates!
These methods let you find areas in various situations, making geometry even more exciting! 🎉
You can use the basic formula mentioned earlier, but you can also explore other methods! For example:
1. Heron’s Formula: This is useful if you know all three side lengths! First, find the semi-perimeter (s = (a + b + c) ÷ 2) and then use the formula Area = √(s × (s - a) × (s - b) × (s - c)).
2. Coordinate Geometry: If you know the vertices' coordinates, you can use the formula involving coordinates!
These methods let you find areas in various situations, making geometry even more exciting! 🎉
Read Less
Real-World Applications of Triangle Area
Triangles have many real-world uses! 🏗
️ Architects use triangle shapes to design buildings because they’re strong! Engineers use triangles in bridges to evenly distribute weight. You’ll also find triangles in art, like pyramids in Egypt! 🏜
️ Did you know that the famous Eiffel Tower in Paris is made using lots of triangular shapes? When you build models or work on crafts, knowing how to calculate the area helps you use materials wisely. Triangles even appear in nature, like in mountain peaks and the shape of certain trees! 🌲
️ Architects use triangle shapes to design buildings because they’re strong! Engineers use triangles in bridges to evenly distribute weight. You’ll also find triangles in art, like pyramids in Egypt! 🏜
️ Did you know that the famous Eiffel Tower in Paris is made using lots of triangular shapes? When you build models or work on crafts, knowing how to calculate the area helps you use materials wisely. Triangles even appear in nature, like in mountain peaks and the shape of certain trees! 🌲
Read Less
Try your luck with the Area Of A Triangle Quiz.
Try this Area Of A Triangle quiz and see how many you score!
Q1
Question 1 of 10
Next
Explore More