Facts for Kids

A circle is a perfectly round shape! 🎡

It has a center point, and all points on the edge are the same distance from that middle point. This distance is called the radius. The area of a circle tells us how much space is inside that circle. We can find it using a special formula! 🍰

Understanding how to calculate the area is not only fun, but it also helps us in real life, like knowing how much paint we need for a round room. Let’s explore the world of circles together! 🌍

Area is the amount of space inside a shape. 🏠

For a circle, it's the space within the curved line that makes up the circle. To find out how much space is in that circle, we use math. The area is measured in square units, like square centimeters (cm²) or square meters (m²). When you draw a circle, you can also think of it like filling a pizza with yummy toppings! 🍕

The whole surface inside is the area, and we need to calculate it to know how many toppings we can add!

You see circles everywhere! 🌍

Look at the sun, the moon, and the wheels on your bicycle! 🚴

‍♀️ Architects use circles in buildings, such as the famous Pantheon in Rome. Engineers design roundabouts on roads to improve traffic flow, and pizza is served in circle shapes! 🍕

Each of these examples shows how the area of a circle helps us understand the world around us in fun and practical ways!

In geometry, circles are very important! 📏

Geometry is the math of shapes and sizes. A circle relates to other geometric figures, like ellipses and polygons. Circles also have interesting parts: the diameter (the distance across the circle) is double the radius. Comparing distances can help us understand shapes better! Many geometric theorems, like the Pythagorean theorem, often involve circles, making it a key subject in math! 🔍

The circle is one of the oldest shapes known to humans, dating back to ancient times! 🏺

The ancient Egyptians and Babylonians used circles in their art and inventions. The Greek mathematician Archimedes helped to find the value of π (pi) around 250 B.C. He knew circles were special, and he explored how to calculate their area. Throughout history, many cultures, including the Romans and Indians, studied circles, making them an important part of math! 📖

Did you know that circles have no corners? ⭐

Circle has an infinite number of lines of symmetry! If you could draw one, you could fold it any way, and both halves would always match up! Also, every circle has a special number – π (pi) – which is about 3.14. 🌈

If you measure the circumference and divide it by the diameter (the width straight across), you will always get π! Isn’t that a cool math trick?

Knowing how to find the area of a circle is useful! 🛠

️ For example, if you want to plant a circular garden, you need to know how much soil you'll need. Or, if you’re making cookies that are round, you can figure out how many can fit on a baking tray. 🎉

Athletes, too, use areas of circles when laying out tracks or designing sports fields. Learning this helps us solve everyday problems, and it’s all thanks to the area of a circle!

The formula for finding the area of a circle is A = πr². 🧮

In this formula, "A" stands for area, "π" (pi) is a special number, about 3.14, and "r" represents the radius! The radius is half the distance across the circle. So, if your circle has a radius of 3 cm, you would multiply 3.14 by 3 (the radius) squared (3 × 3). This means you will calculate it as A = 3.14 x 9 = 28.26 cm²! 📏

Circles connect to other fun math ideas! 🔗

For instance, the circumference is the distance around a circle and can be calculated using the formula C = 2πr. 💡

There are also chords (lines connecting two points on a circle) and arcs (part of the circle). Understanding these helps us learn about angles and rotations, which are super important in algebra and trigonometry! 🎓

Mathematics is like a puzzle, and circles are a big piece of it!

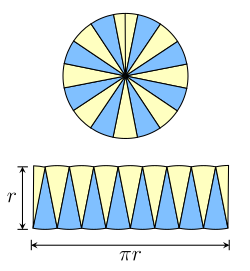
To understand why A = πr² makes sense, we can use a fun idea! Imagine cutting the circle into lots of small triangles that point towards the center. 🌟

If we count all those tiny triangles and arrange them, they almost look like a rectangle! The base of this rectangle is the circle's circumference (the distance around it), and the height is the radius. Since the circumference can be found using 2πr, we can say the area ends up being about half of that times the radius: 1/2 x circumference x radius, leading us to A = πr²!